Topology > Base
Definition:
Let  be a topological space. A collection
be a topological space. A collection 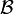 of open sets is called a base for the topology
of open sets is called a base for the topology  if every open set
if every open set  is the union of sets in
is the union of sets in 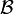 .
.
 be a topological space. A collection
be a topological space. A collection 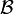 of open sets is called a base for the topology
of open sets is called a base for the topology  if every open set
if every open set  is the union of sets in
is the union of sets in 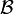 .
.
Obviously  is a base for itself.
is a base for itself.
 is a base for itself.
is a base for itself.Conditions for being a base:
In a topological space  a collection
a collection 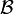 is a base for
is a base for  if and only if it consists of open sets and for each point
if and only if it consists of open sets and for each point  and open neighborhood
and open neighborhood  of
of  there is a set
there is a set  such that
such that  .
.
 a collection
a collection 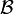 is a base for
is a base for  if and only if it consists of open sets and for each point
if and only if it consists of open sets and for each point  and open neighborhood
and open neighborhood  of
of  there is a set
there is a set  such that
such that  .
.Constructing topologies from base:
Let  be any set and
be any set and 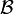 a collection of subsets of
a collection of subsets of  . There exists a topology
. There exists a topology  on
on  such that
such that 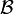 is a base for
is a base for  if and only if
if and only if 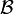 satisfies the following:
satisfies the following:
 be any set and
be any set and 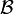 a collection of subsets of
a collection of subsets of  . There exists a topology
. There exists a topology  on
on  such that
such that 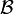 is a base for
is a base for  if and only if
if and only if 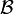 satisfies the following:
satisfies the following:- If
 , then there exists a
, then there exists a  such that
such that 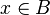 .
. - If
 and
and  , then there is a
, then there is a  such that
such that  .
.
Remark : Note that the first condition is equivalent to saying that The union of all sets in 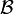 is
is  .
.
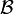 is
is  .
.Semibasis:
Let  be any set and
be any set and 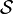 a collection of subsets of
a collection of subsets of  . Then
. Then 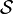 is a semibase if a base of X can be formed by a finite intersection of elements of
is a semibase if a base of X can be formed by a finite intersection of elements of 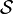 .
.
 be any set and
be any set and 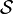 a collection of subsets of
a collection of subsets of  . Then
. Then 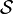 is a semibase if a base of X can be formed by a finite intersection of elements of
is a semibase if a base of X can be formed by a finite intersection of elements of  .
.